数智化大会PPT

40页农业教育可视化数据PPT图表合集
页数：40 | 大小：24M
40页农业教育可视化数据PPT图表合集由麦克PPT网提供下载，这套PPT以教育和农业生产元素为主，适用于教育行业和农业行业。
40页多彩数据分析专用可视化PPT图表合集
页数：41 | 大小：5M
40页多彩数据分析专用可视化PPT图表合集由麦克PPT网提供下载，这款PPT图表采用了欧美风格，多彩的元素，可用于多种PPT场合。
2022年小学数学新课标变化与解读PPT模板
页数：36 | 大小：8M
PPT模板展示了小学数学新课标变化与解读课件内容，模板详细解读了小学数学新课标的变化，教学总是围绕课程标准来进行，学校以及老师都应时刻关注课程标准，对于其变化与更新及时解读，并根据变化对教学内容和方向进行调整。模板对于小学数学新课标变化的解读有利于学校和老师及时调整相关内容，对新课标有一个整体上的把握。
少数民族文化之维吾尔族介绍PPT课件
页数：27 | 大小：86M
PPT模板主要从四个部分介绍了维吾尔族的民族文化，首先介绍了维吾尔族的名称和历史。这一名称有团结、联合、协助的意思。从公元四世纪就有对维吾尔族的记载。第二部分介绍了维吾尔族的文化常识，包括尔族的宗教信仰、饮食文化、服饰文化、建筑文化、语言与文字、民间文学等。第三部分建设了维吾尔族的艺术形式，维吾尔族人民能歌善舞，有具有民族特色的民歌舞蹈。最后介绍了维吾尔族的习俗。
义务教育数学课程标准变化与解读PPT课件
页数：36 | 大小：8M
这个PPT主要分为六个部分。PPT的第一个部分向我们介绍的是。PPT的第二个部分向我们介绍的是等等内容。PPT的第三个部分向我们介绍的是等等内容。PPT的第四个部分向我们介绍的是等等内容。PPT的第五个部分向我们介绍的是。PPT的第六个部分向我们介绍的是。课程标准修订的总体方案与基本原则，数学核心素养理念的解读，小学数学课程新的变化趋势对学生思维能力培养的关注。
高中数学1.4《生活中的优化问题》PPT课件
页数：12 | 大小：3M
PPT模板从四个部分来展开介绍关于《生活中的优化问题》的教学内容。PPT模板的第一部分介绍了解决实际应用问题的四个基本步骤。第二部分介绍了求实际问题中的最大值或者最小值的三个基本解题步骤。第三部分阐述了应用问题和优化问题的含义。第四部分介绍了解决体积（容积）最大和费用最省的相关题目的解题思路和解题技巧，并展示了相关解题过程。
小学六年级下册数学面积的变化PPT课件
页数：23 | 大小：5M
本套PPT模板在内容上首先介绍了本节课的教学内容，点明了本节课的重点和难点，提出问题，激发学生的学习兴趣；接着以长方形的长宽变化预估长方形面积变化的比例，并计算得出结果；然后将三角形、正方形、圆面积变化与底边与高、长宽、半径变化的关系，测算放大后与放大前的比值，并通过表格展示出来；最后寻找表格中的比值规律，得出面积比与长度比的关系；
苗族少数民族文化习俗介绍PPT课件模板
页数：13 | 大小：4M
这个PPT主要分为六个部分。PPT的第一个部分向我们介绍的是苗族的简介，包括名称来历，发展历史、进程、影响分布的情况。PPT的第二个部分向我们介绍的是苗族的舞蹈等等内容。PPT的第三个部分向我们介绍的是苗族的舞蹈分类等等内容。PPT的第四个部分向我们介绍的是苗族舞蹈的特征，包括自愈性，习俗性，表演性等等内容。PPT的第五个部分向我们介绍的是。PPT的第六个部分向我们介绍的是苗族舞蹈的分类。
少数民族文化之维吾尔族介绍PPT课件
页数：26 | 大小：34M
这份PowerPoint由四个部分构成。第一部分内容是民族简介，PPT模板一方面介绍了维吾尔和维吾尔族的概念，另一方面是维吾尔族主要居住地。第二部分内容是饮食文化，这一部分主要介绍了传统饮食，其中包括馕、抓饭、蒸包子、拉面和饮茶。第三部分内容是婚葬习俗，这一部分首先介绍了自由恋爱，其次是丧葬的习俗。第四部分内容是传统节日，包括开斋节、古尔邦节、诺鲁孜节和玫瑰节。第五部分内容是谎言与真相。
数学质量分析与优化之路PPT课件免费下载
页数：30 | 大小：17M
PPT模板内容主要通过PowerPoint软件分四个部分来向我们展开介绍有关于数学质量分析与优化课件的相关内容。PPT模板内容第一部分主要向我们详细的介绍了学科命题的相关特点。第二部分主要向我们详细的讲解了有关于数学命题的主要导向。第三部分主要给我们分析了数学比较典型的一些错题。第四部分主要向我们详细的讲述了我们应该如何去改进和优化数学质量的具体内容。
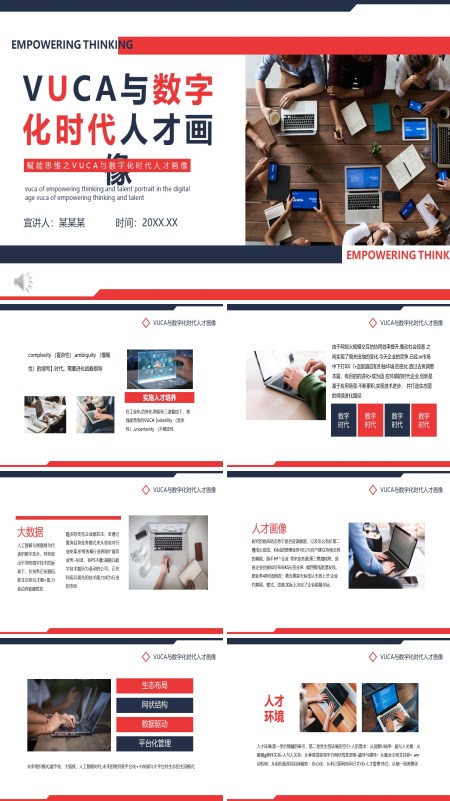
赋能思维之vuca与数字化时代人才画像培训PPT
页数：15 | 大小：14M
这份PowerPoint由四个部分构成。第一部分内容是实施人才培养，该模板首先对VUCA的概念进行阐述。第二部分内容是数字时代，这一部分首先介绍了大数字背景，其次是人才画像，最后对未来的组织模式进行简要说明。第三部分内容是人才环境和公司战略，这一部分主要包括确定目标公司、大中客户经理人才画像。第四部分内容是构建新人才画像，包括基本信息、网络关系、专业领域和专业表现。
少数民族壮族文化习俗知识课件PPT模板
页数：31 | 大小：36M
PPT模板内容主要通过PowerPoint软件分五个部分来向我们展开介绍有关于壮族民族文化宣传课件的相关内容。PPT模板内容第一部分主要向我们详细的介绍了壮族的相关服饰特点。第二部分主要是有关于壮族的简介。第三部分主要向我们详细的讲述了有关于壮族的建筑特点。第四部分主要向我们详细的讲述了有关于壮族的相关饮食习惯。最后一部分主要向我们阐述了壮族的传统节日。
文化科普介绍少数民族黎族民俗PPT课件
页数：20 | 大小：25M
本套PPT模板在内容上分为地理分布与由来、黎族风俗与习惯、特色建筑和服饰、民族的饮食文化共计四个部分；第一部分首先介绍了黎族的由来，黎族是海南岛最早的居民，主要分布在海南省各县市，部分散居在贵州省等；第二部分介绍了黎族人的礼仪、信仰、婚姻和节日等；第三部分介绍了黎族的特色建筑，包括船型屋、金字形茅屋、谷仓等等，以及黎族的传统服饰；第四部分介绍了黎族的饮食文化；
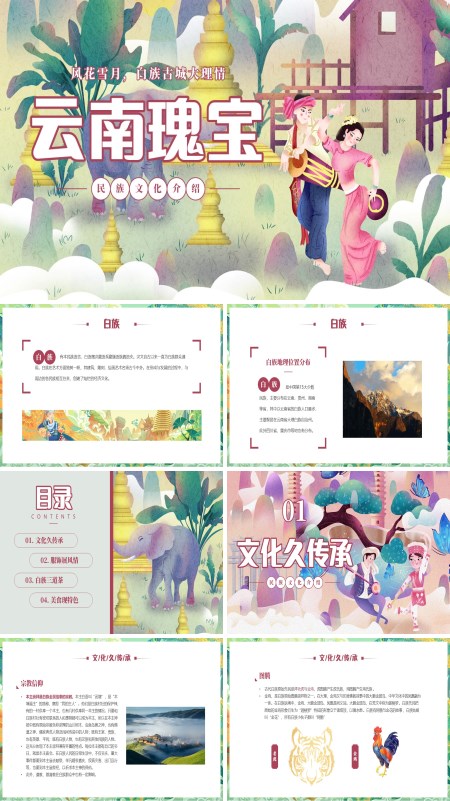
白族民俗文化科普少数民族知识介绍PPT课件
页数：28 | 大小：36M
PowerPoint从四个部分来展开介绍关于少数民族白族民俗文化科普知识的相关内容。PPT模板的第一个部分为文化久传承，运用幻灯片介绍了白族的宗教信仰、图腾、诗歌、绘画等内容。第二个部分主题为服饰展风情，通过演示文稿展示了白族飘带为主要特色的民族服饰以及白族的首饰、头巾、头饰、秀鞋等内容。第三个部分分享了白族的三道茶。第四个部分展示了白族的特色美食，包括生皮乳扇、大理砂锅鱼、粑粑等。
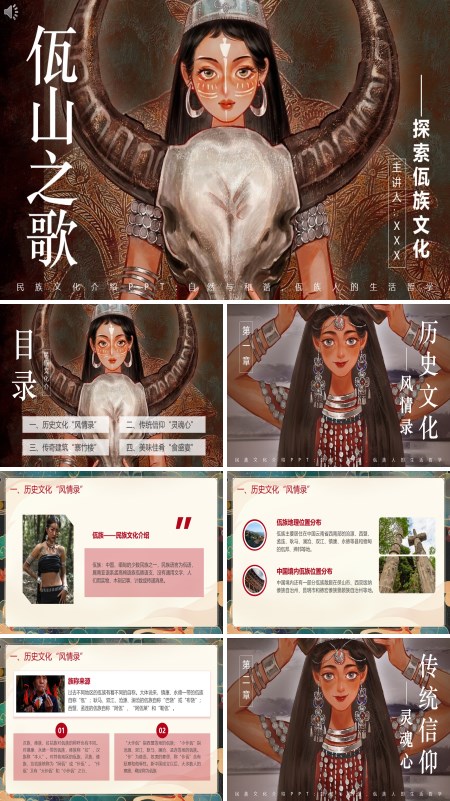
佤族民俗文化少数民族科普介绍PPT课件
页数：26 | 大小：20M
此PPT模板将探索佤族文化分为四个部分进行展开。第一部分是历史文化风情录，这一部分主要介绍了佤族地理位置分布和族称来源。第二部分是传统信仰灵魂心，这一部分介绍了佤族最具特点的信仰，同时还介绍了佤族信仰的佛教和基督教。第三部分是传奇建筑寨竹楼，这一部分介绍了佤族的建筑特色。第四部分是美味佳肴食盛宴的相关介绍。
含讲稿

教师数字化转型理解与感悟PPT课件模板含讲稿
页数：22 | 大小：20M
这是一套关于教师数字化转型理解与感悟的PPT，共包含21页。在当今时代，信息技术的飞速发展正深刻地改变着各个行业和领域的工作模式，教育领域也不例外。教师作为教育的主力军，既迎来了前所未有的机遇，也面临着诸多挑战。为了更好地适应数字化时代的需求，教师需要不断提升自身的专业能力，积极参加数字化转型培训，持续更新知识体系，并学会有效利用网络资源来提升专业水平。这一过程对于教师专业素养的提升具有极为重要的意义。该PPT由五个部分构成。第一部分聚焦于数字化转型的背景与趋势，首先介绍了教育领域在数字化浪潮下的变革历程，随后深入分析了教师在这一过程中所面临的挑战与机遇。第二部分探讨教师数字化转型的内涵，从理念更新、资源运用和技能提升三个方面展开，明确了教师转型的关键方向。第三部分通过实践案例展示，一方面呈现了国内学校在教师数字化转型方面的成功经验，另一方面也介绍了国外教师的转型之路，为观众提供了丰富的参考。第四部分提出了教师数字化转型的策略与建议，为教师在转型过程中可能遇到的问题提供了实用的解决方案。第五部分则是对教师数字化转型的未来展望，展望了数字化教育发展的方向以及教师在其中的潜在角色。通过这五个部分的系统阐述，PPT不仅帮助教师深入了解数字化转型的必要性和紧迫性，还为他们在转型过程中提供了清晰的思路和方法，助力教师在数字化时代更好地履行教育使命，推动教育事业的高质量发展。
含教案

数学北师大八年级上第四章 4.2认识一次函数第3课时一次函数在计费问题中的应用（教学课件）ppt课件含教案
页数：22 | 大小：3M
这份由二十二张幻灯片构成的PPT课件，专为北师大版八年级上册第四章《4.2 认识一次函数》第3课时“一次函数在计费问题中的应用”量身定制。课程以“复习—探究—巩固—小结”四步递进，旨在让学生把“一次函数”从纸上的符号变成生活里的“计费神器”。开篇“知识回顾”用快闪方式唤醒记忆：教师抛出y=kx+b的解析式，学生口答k与b的现实意义，随后屏幕滚动呈现“斜率即单价、截距即起步价”的口诀，为后续应用奠定概念锚点。进入“新知探究”，课件切换到课本例题“出租车计价”：起步价10元含3公里，之后每公里2元。学生分组填表记录里程x与车费y，发现3公里后“每多1公里，多2元”，变化率恒定，教师顺势引导列式y=2(x−3)+10，化简得y=2x+4，学生亲眼看到“一次函数=计费规则”的诞生过程。紧接着头脑风暴：水费阶梯、快递超重、共享充电宝计时……每组选取一个场景，现场测量数据并写出解析式，派代表登台讲解，台下同学用点赞贴纸投票“最会省钱方案”，课堂瞬间化身“计费创意市集”。 “基础巩固”分层推进：A层直接代入解析式求费用；B层给出预算反推可行驶最大里程，需解一元方程；C层引入“两段计价”真题，要求写出分段函数并画图像，平板实时生成正确率热力图，教师针对红区错误现场“开刀”。结课用“电梯演讲”——30秒说清一次函数在计费里的作用，弹幕滚成词云；作业分两层：A层完成教材配套练习，B层记录家庭本月电费单，按“阶梯单价”写出一次函数模型并预测下月费用，把课堂所学搬回家。整套课件通过“生活场景—数据提炼—模型建构—即时反馈”的闭环设计，不仅让学生真正理解“一次函数就是单价数量+起步价”的计费本质，更在“算钱、省钱、比方案”的实战中，显著提升模型意识与应用能力，为后续学习分段函数、不等式及优化问题奠定坚实的方法与情感双重基础。
含教案

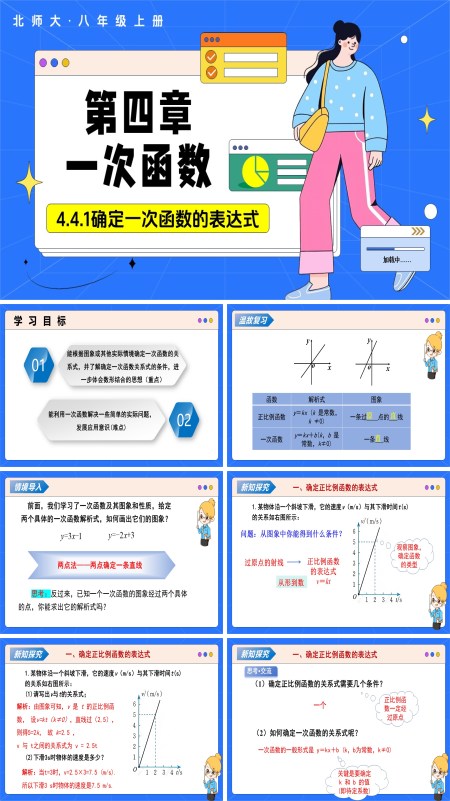
数学北师大八年级上册第四章 4.4一次函数的应用（第1课时确定一次函数的表达式）（教学课件）ppt课件含教案
页数：16 | 大小：3M
这份共十六张的PPT课件，紧扣北师大版八年级上册第四章《一次函数的应用》第一课时——“确定一次函数的表达式”，以“会看图、会设式、会求参”为核心目标，引导学生在图像与情境中还原解析式，深刻体验数形结合的魅力。课堂仍循五步展开：温故—情境—新知—典例—小结。“温故复习”用快闪方式唤醒记忆：正比例函数y＝kx的图像必过原点，一次函数y＝kx＋b的斜率k定方向、截距b定位置，学生边口述边用手势比斜率，教师顺势板书“两点定一线”，为后续求参埋下伏笔。“情境导入”给出两条已画直线：y＝2x＋1与y＝－x＋3，让学生抢答“谁先画到y轴1？谁与x轴交于-3？”在温习图像特征的同时，教师追问：“如果反过来，已知直线经过(0,4)和(2,0)，你能写出它的解析式吗？”问题一转，引出本课核心任务——由图或情境确定表达式。“新知探究”分两步走：先特殊后一般。①确定正比例函数：给出图像过点(3,6)，学生口算k＝2，写出y＝2x，归纳“一个非原点即可定k”；②确定一次函数：给出图像与y轴交于-1，且过点(2,3)，学生先写y＝kx－1，再代入求k＝2，归纳“两点或一点加截距可定k、b”。教师随即用GeoGebra动态演示：拖动两点，解析式实时变化，学生眼见“点动式动”，深刻感受坐标与参数的对应关系。“典例巩固”采用“一题三问”：给出一次函数图像与坐标轴两交点，先写解析式，再求x＝-1时的函数值，最后判断点(m,m+2)是否在图像上，平板实时统计正确率，教师针对红区错误现场“开刀”；随后推送中考真题切片，给出实际情境“租车计费”，要求先设y＝kx＋b，再利用两组数据求参，实现“情境→图像→解析式”的完整闭环。结课用“思维导图快闪”：两点坐标→列方程组→解k、b→写解析式四步一气呵成，学生口头接龙补充易错点；作业分两层：A层完成教材配套“由图求式”练习，B层拍摄家中电表读数，记录两次时间与示数，写出一次函数模型并预测下次读数，把课堂所学搬回家。整套课件通过“动态演示—即时求参—情境回归”的闭环设计，不仅让学生真正掌握“两点定一线”的求法，更在“看图像→写解析式→回代检验”的反复实践中，深刻体会数形结合思想，为后续学习一次函数与方程、不等式综合应用奠定坚实的模型与思维双重基础。
含教案

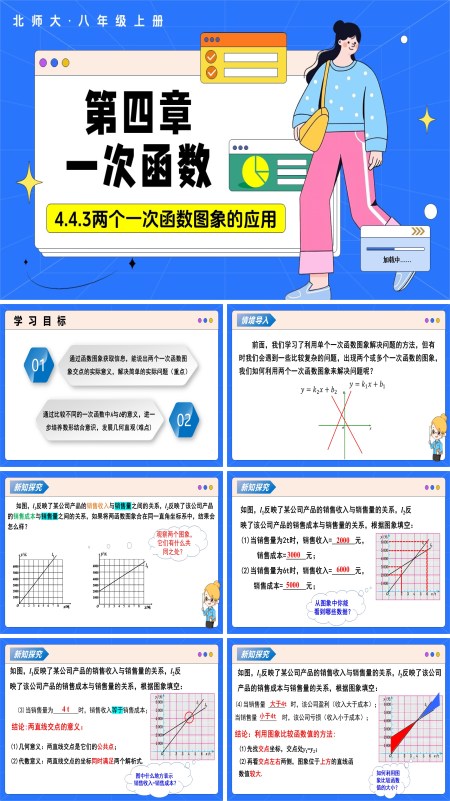
数学北师大八年级上第四章 4.4一次函数的应用（第3课时两个一次函数图象的应用）（教学课件）ppt课件含教案
页数：22 | 大小：5M
这套由二十二张幻灯片构成的教学课件，紧扣北师大版八年级上册第四章《一次函数的应用》第三课时，聚焦“两个一次函数图像的交点”这一核心，引领学生从“看图说话”走向“借图解题”，体会交点背后的实际意义。课堂流程简洁而递进：情境导入—新知探究—典例变式—课堂小结。“情境导入”抛出学生熟悉的“租车比价”场景：A公司收固定起步费加每公里租金，B公司免起步费但单价略高。屏幕同时呈现两家公司的路程—费用折线图，教师提问：“什么时候两家价钱相同？哪段路程选哪家更划算？”生活化悬念瞬间点燃探究欲望，学生直观发现“两条线交叉”即为关键节点，自然引出本课核心——两个一次函数图像交点的实际含义。“新知探究”分三步走：①读图——用GeoGebra动态显示y＝k₁x＋b₁与y＝k₂x＋b₂的交点，学生眼见横坐标x₀使两函数值相等；②释义——教师引导得出“交点横坐标即两方案费用相等时的路程，纵坐标即此时的共同费用”，把抽象的‘解方程组’转化为可视的‘两线相遇’；③决策——拖动x轴上的动点，左侧y₁y₂、右侧y₁y₂，学生立刻体会“哪条线低就选哪家”的优化思想，实现“交点分界、左右比价”的建模思路。“典例变式”采用“一景三问”：给出“水费阶梯计价”双段折线图，先求交点坐标，再解释交点含义，最后设计用水量使费用最低，平板实时统计正确率，教师针对红区错误现场“开刀”；随后推送中考真题，要求用双图像法与代数法并列求“两车队运费相等”的临界点，实现“情境→图像→方程→决策”的完整闭环。结课用“思维导图快闪”：两直线→交点→横坐标相等→实际意义四步一气呵成，学生口头接龙补充易错点；作业分两层：A层完成教材配套“读交点”练习，B层观察家用水电费账单，绘制两段计价直线并求交点，说明如何用水用电最省钱，把课堂所学搬回家。整套课件通过“动态交点—即时释义—左右比价”的闭环设计，不仅让学生真正掌握“两线交点=方程组的解=现实决策临界点”的核心思想，更在“看图→找点→释义→择优”的反复实践中，深刻体会数形结合的魅力，为后续学习不等式组、线性规划奠定坚实的模型与思维双重基础。
炫彩MBE风格互联网大数据创意培训课件PPT模板
页数：26 | 大小：4M
炫彩MBE风格互联网大数据创意培训课件PPT模板，采用现在比较流行的MBE风格，这种风格的特色是色彩鲜艳，整体风格比较Q，或者说是一种比较呆萌的风格。