-
中国少年先锋队第十次代表大会PPT少先队少代会流程专题课件模板
页数：38 | 大小：22M这个PPT主要分为十四个部分。PPT的第一个部分是共同奏唱国歌。第二个部分是共同奏唱队歌。第三个部分是代表少先队员进行献词。第四个部分是学校领导致辞。第五个部分是对优秀集体和个人进行表彰。第六个部分是做进行工作报告。第七个部分是竞选大队委员。第八个部分是选举学校的少工委。第九个部分是对不同项目的提案和展示。第十个部分是通过决议的报报告。第十一个部分是任队委授标志。第十二个部分是宣读倡议书。第十三个部分是少工委的领导讲话。第十个四个部分是宣布退旗。
-
含讲稿
解读中国社会主义青年团第一次全国代表大会PPT专题党课
页数：19 | 大小：13M这个PPT主要分为三个部分。PPT的第一个部分向我们介绍的是团一大召开的过程，包括召开的时间、闭幕时间、大会的意义、解决的问题。第二个部分向我们介绍的是团一大在广东召开的主要原因：包括广东独特的政治环境，共产党对广东青年运动的重视、马克思主义在广东的广泛传播等等。第三个部分向我们介绍的是团一大的重要意义等等。
-
从十八届一中全会到七中全会深入解读十九大报告PPT模板
页数：22 | 大小：14M党的十九大是在全面建成小康社会关键阶段、中国特色社会主义发展关键时期召开的一次十分重要的大会，对鼓舞和动员全党全国各族人民继续推进全面建成小康社会、坚持和发展中国特色社会主义具有重大意义。
-
八论学习贯彻党的十九届六中全会精神PPT党课课件
页数：58 | 大小：13M该PPT以八论学习贯彻党的十九届六中全会精神为主题，内容上，从八个方面论述主题，第一个深刻把握党百年奋斗的重大成就，第二深刻理解党百年奋斗的历史意义，第三是深刻领会党百年奋斗的历史经验，第四是深化对新时代党的创新理论的理解和掌握，第五是深刻领悟加强党的政治建设这个鲜明特征和政治优势，第六是深刻认识党同人民生死相依休戚与共的血肉联系，第七是增强全面从严治党永远在路上的坚定和执着。最后是锚定既定奋斗目标意气风发走向未来。
-
人教版九年级《二次函数与一元二次方程》教学课件PPT
页数：21 | 大小：6MPPT主要展示了初中数学人教版九年级《二次函数与一元二次方程》教育教学的主题内容。PPT的整体色调以墨蓝色以及白色为主，将教师站在讲台上讲解知识的形象、纸飞机、云朵、深蓝色色块以及与教学主题内容有关的图片作为主要装饰，给人以专业明了之感。PPT的主要内容包括教学目标、回顾旧知、教学重难点、实际问题、探究二次函数与一元二次方程的关系、课堂小结以及作业等几个部分的内容。旨在通过这节课的学习，让学生掌握有关二次函数的相关知识。
-
含教案
人教版数学九年级上册二次函数与一元二次方程PPT课件含教案
页数：43 | 大小：3M这份PPT由四个部分组成。第一部分内容是导入新知和素养目标，学生首先会利用二次函数的图象求一元二次方程的近似解，其次能够理解二次函数与一元二次方程的根的个数之间的关系，最后可以体会方程与函数之间的联系。第二部分内容是探究新知，这一部分主要包括二次函数与一元二次方程的关系、两者关系在实际生活中的应用、一元二次方程的图象解法。第三部分内容是课堂检测，这一部分一方面展示了五道基础巩固题，另一方面是对能力提升题进行展示。第四部分内容是课堂小结和课后作业。
-
二次元知识介绍PPT课件免费下载
页数：21 | 大小：10M这份PowerPoint由四个部分构成。第一部分内容是基本概念，该模板首先对次元和二次元的定义进行阐述。第二部分内容是发展起源，这一部分首先介绍了二次元的最早起源和寓意，其次是从广义上来分析。第三部分内容是兴起原因，这一部分主要包括政策支持、移动互联网的发展和进入90后时代。第四部分内容是引申词含义，包括按世界、个性文化、萌二文化、载体来划分。
-
第五次全国经济普查PPT专题党课
页数：21 | 大小：7MPPT党课从六个方面介绍了有关第五次全国经济普查党课的相关内容。第一部分内容是概念与历史。第二部分内容是目的与意义，为宏观调控提供可靠依据、为常规统计提供必要条件、为国民经济核算提供全面翔实的基础数据、为地区，企业和个人生产经营提供参考。第三部分内容是对象与范围，包括在我国境内从事第二产业和第三产业的全部法人单位产业活动单位和个体经营户，具体行业包括采矿业、制造业、电力、热力、燃气等。第四部分内容是方法与流程。第五部分内容是组织与实施。第六部分内容是疑问与解答。
-
2023第五次全国经济普查PPT课件
页数：20 | 大小：11MPPT模板内容主要通过PowerPoint软件分六个部分来向我们详细的讲述有关第五次经济普查的内容，共计21张幻灯片。PPT模板内容第一部分主要向我们详细的阐述了有关经济普查的概念与历史的内容。第二部分是经济普查的目的与意义的相关内容。第三部分是经济普查的对象与范围的相关内容。第四部分是经济普查的方法与流程。第五部分是经济普查的组织与实施。第六部分是疑问和解答的相关内容。
-
会议座次礼仪培训课件PPT模板
页数：11 | 大小：4M这个PPT主要分为六个部分。PPT的第一个部分向我们介绍的是在会议当中应当如何合理安排座次。第二个部分向我们介绍的是安排出席者位置要注意哪些方面的问题。第三个部分向我们介绍的是接待会议人员应当注意的问题。第四个部分向我们介绍的是社交场合排列座次的五大技巧。第五个部分向我们介绍的是会议主席台座次的安排。第六个部分向我们介绍的是主席台座次安排表。
-
含教案
数学北师大八年级上第四章 4.2认识一次函数 第3课时一次函数在计费问题中的应用（教学课件）ppt课件含教案
页数：22 | 大小：3M这份由二十二张幻灯片构成的PPT课件，专为北师大版八年级上册第四章《4.2 认识一次函数》第3课时“一次函数在计费问题中的应用”量身定制。课程以“复习—探究—巩固—小结”四步递进，旨在让学生把“一次函数”从纸上的符号变成生活里的“计费神器”。开篇“知识回顾”用快闪方式唤醒记忆：教师抛出y=kx+b的解析式，学生口答k与b的现实意义，随后屏幕滚动呈现“斜率即单价、截距即起步价”的口诀，为后续应用奠定概念锚点。 进入“新知探究”，课件切换到课本例题“出租车计价”：起步价10元含3公里，之后每公里2元。学生分组填表记录里程x与车费y，发现3公里后“每多1公里，多2元”，变化率恒定，教师顺势引导列式y=2(x−3)+10，化简得y=2x+4，学生亲眼看到“一次函数=计费规则”的诞生过程。紧接着头脑风暴：水费阶梯、快递超重、共享充电宝计时……每组选取一个场景，现场测量数据并写出解析式，派代表登台讲解，台下同学用点赞贴纸投票“最会省钱方案”，课堂瞬间化身“计费创意市集”。 “基础巩固”分层推进：A层直接代入解析式求费用；B层给出预算反推可行驶最大里程，需解一元方程；C层引入“两段计价”真题，要求写出分段函数并画图像，平板实时生成正确率热力图，教师针对红区错误现场“开刀”。 结课用“电梯演讲”——30秒说清一次函数在计费里的作用，弹幕滚成词云；作业分两层：A层完成教材配套练习，B层记录家庭本月电费单，按“阶梯单价”写出一次函数模型并预测下月费用，把课堂所学搬回家。整套课件通过“生活场景—数据提炼—模型建构—即时反馈”的闭环设计，不仅让学生真正理解“一次函数就是单价数量+起步价”的计费本质，更在“算钱、省钱、比方案”的实战中，显著提升模型意识与应用能力，为后续学习分段函数、不等式及优化问题奠定坚实的方法与情感双重基础。
-
含教案
数学北师大八年级上册第四章 4.4一次函数的应用（第1课时确定一次函数的表达式）（教学课件）ppt课件含教案
页数：16 | 大小：3M这份共十六张的PPT课件，紧扣北师大版八年级上册第四章《一次函数的应用》第一课时——“确定一次函数的表达式”，以“会看图、会设式、会求参”为核心目标，引导学生在图像与情境中还原解析式，深刻体验数形结合的魅力。课堂仍循五步展开：温故—情境—新知—典例—小结。“温故复习”用快闪方式唤醒记忆：正比例函数y＝kx的图像必过原点，一次函数y＝kx＋b的斜率k定方向、截距b定位置，学生边口述边用手势比斜率，教师顺势板书“两点定一线”，为后续求参埋下伏笔。“情境导入”给出两条已画直线：y＝2x＋1与y＝－x＋3，让学生抢答“谁先画到y轴1？谁与x轴交于-3？”在温习图像特征的同时，教师追问：“如果反过来，已知直线经过(0,4)和(2,0)，你能写出它的解析式吗？”问题一转，引出本课核心任务——由图或情境确定表达式。“新知探究”分两步走：先特殊后一般。①确定正比例函数：给出图像过点(3,6)，学生口算k＝2，写出y＝2x，归纳“一个非原点即可定k”；②确定一次函数：给出图像与y轴交于-1，且过点(2,3)，学生先写y＝kx－1，再代入求k＝2，归纳“两点或一点加截距可定k、b”。教师随即用GeoGebra动态演示：拖动两点，解析式实时变化，学生眼见“点动式动”，深刻感受坐标与参数的对应关系。“典例巩固”采用“一题三问”：给出一次函数图像与坐标轴两交点，先写解析式，再求x＝-1时的函数值，最后判断点(m,m+2)是否在图像上，平板实时统计正确率，教师针对红区错误现场“开刀”；随后推送中考真题切片，给出实际情境“租车计费”，要求先设y＝kx＋b，再利用两组数据求参，实现“情境→图像→解析式”的完整闭环。结课用“思维导图快闪”：两点坐标→列方程组→解k、b→写解析式四步一气呵成，学生口头接龙补充易错点；作业分两层：A层完成教材配套“由图求式”练习，B层拍摄家中电表读数，记录两次时间与示数，写出一次函数模型并预测下次读数，把课堂所学搬回家。整套课件通过“动态演示—即时求参—情境回归”的闭环设计，不仅让学生真正掌握“两点定一线”的求法，更在“看图像→写解析式→回代检验”的反复实践中，深刻体会数形结合思想，为后续学习一次函数与方程、不等式综合应用奠定坚实的模型与思维双重基础。
-
含教案
数学北师大八年级上第四章 4.4一次函数的应用（第3课时两个一次函数图象的应用）（教学课件）ppt课件含教案
页数：22 | 大小：5M这套由二十二张幻灯片构成的教学课件，紧扣北师大版八年级上册第四章《一次函数的应用》第三课时，聚焦“两个一次函数图像的交点”这一核心，引领学生从“看图说话”走向“借图解题”，体会交点背后的实际意义。课堂流程简洁而递进：情境导入—新知探究—典例变式—课堂小结。“情境导入”抛出学生熟悉的“租车比价”场景：A公司收固定起步费加每公里租金，B公司免起步费但单价略高。屏幕同时呈现两家公司的路程—费用折线图，教师提问：“什么时候两家价钱相同？哪段路程选哪家更划算？”生活化悬念瞬间点燃探究欲望，学生直观发现“两条线交叉”即为关键节点，自然引出本课核心——两个一次函数图像交点的实际含义。“新知探究”分三步走：①读图——用GeoGebra动态显示y＝k₁x＋b₁与y＝k₂x＋b₂的交点，学生眼见横坐标x₀使两函数值相等；②释义——教师引导得出“交点横坐标即两方案费用相等时的路程，纵坐标即此时的共同费用”，把抽象的‘解方程组’转化为可视的‘两线相遇’；③决策——拖动x轴上的动点，左侧y₁y₂、右侧y₁y₂，学生立刻体会“哪条线低就选哪家”的优化思想，实现“交点分界、左右比价”的建模思路。“典例变式”采用“一景三问”：给出“水费阶梯计价”双段折线图，先求交点坐标，再解释交点含义，最后设计用水量使费用最低，平板实时统计正确率，教师针对红区错误现场“开刀”；随后推送中考真题，要求用双图像法与代数法并列求“两车队运费相等”的临界点，实现“情境→图像→方程→决策”的完整闭环。结课用“思维导图快闪”：两直线→交点→横坐标相等→实际意义四步一气呵成，学生口头接龙补充易错点；作业分两层：A层完成教材配套“读交点”练习，B层观察家用水电费账单，绘制两段计价直线并求交点，说明如何用水用电最省钱，把课堂所学搬回家。整套课件通过“动态交点—即时释义—左右比价”的闭环设计，不仅让学生真正掌握“两线交点=方程组的解=现实决策临界点”的核心思想，更在“看图→找点→释义→择优”的反复实践中，深刻体会数形结合的魅力，为后续学习不等式组、线性规划奠定坚实的模型与思维双重基础。
-
共青团十八大会议PPT模板
页数：24 | 大小：10M共青团十八大会议PPT模板分为：1、共青团十八大会议背景；2、共青团十八大主要内容；3、共青团十八大重要意义；4、做有担当的新时代新青年。
-
含教案
一着惊海天——目击我国航母舰载战斗机首架次成功着舰语文八年级上册PPT课件含教案
页数：25 | 大小：8MPPT模板从四个部分来展开介绍关于人教版八年级上册语文课文《一着惊海天——目击我国航母舰载战斗机首架次成功着舰》的相关内容。PPT模板的第一部分展示了本文的生字读音以及生词释义。第二部分阐述了通讯的定义以及通讯的三大特点，并介绍了通讯的分类、第三部分概述了本文的主要内容，并分析了其文章内涵。第四部分展示了本节课的板书设计。
-
含教案
五年级数学下册第八单元第02课时稍复杂的找次品问题PPT课件含教案
页数：31 | 大小：7M这是一套关于“稍复杂的找次品问题第2课时”的演示文稿，共包含31张幻灯片。在本节课中，教师将通过精心设计的教学环节，引导学生深入探究找次品的最优策略。通过解决与本堂课知识相关的数学问题，学生不仅能够掌握高效解决问题的方法，还能深刻体会到数学知识的实用性和简洁性。这种教学方式能够帮助学生在面对复杂问题时，迅速找到解决问题的关键，从而提高他们的数学思维能力和解决问题的能力。演示文稿分为五个部分。第一部分是学习目标和重点难点。在这一部分中，教师明确了本节课的学习目标，让学生清楚地知道本节课需要掌握的知识和技能。同时，教师还指出了学习的重点和难点，帮助学生在学习过程中有的放矢，集中精力攻克关键问题。通过明确目标和重点难点，学生能够更好地把握学习方向，提高学习效率。第二部分是课前导入。这一部分首先通过练习的方式复习了已学知识，帮助学生巩固之前学习的内容，为本节课的学习做好铺垫。接着，教师介绍了找次品的基本思路，引导学生回顾之前所学的方法，并在此基础上进行拓展和深化。通过复习和引入新知识，学生能够更好地衔接新旧知识，为后续的学习打下坚实的基础。第三部分是学习任务。这一部分是本节课的核心内容，旨在培养学生解题思路和做题技巧。通过精心设计的学习任务，教师引导学生逐步探索找次品的最优策略。学生在完成任务的过程中，能够学会如何分析问题、寻找规律，并运用优化的数学方法解决数学问题。这一过程不仅能够提高学生的解题能力，还能培养他们的逻辑思维能力和创新意识。同时，通过解决实际问题，学生能够感受到数学知识的魅力和实用性，进一步激发他们学习数学的兴趣。第四部分是达标练习。在这一部分中，教师设计了一系列与本节课知识相关的练习题，帮助学生巩固所学知识，检验学习成果。通过练习，学生能够加深对找次品最优策略的理解和掌握，提高解题的准确性和速度。同时，教师可以通过学生的练习情况，及时发现学生在学习过程中存在的问题，并进行针对性的指导和讲解，帮助学生进一步完善知识体系，提高学习效果。第五部分是知识总结。在这一部分中，教师对本节课所学的知识进行了系统的梳理和总结。通过回顾本节课的学习内容，学生能够清晰地了解本节课的重点知识和解题方法，加深对知识的理解和记忆。同时，教师还可以引导学生总结学习过程中的经验和教训，帮助学生进一步提升思维能力和学习方法。通过知识总结，学生能够更好地把握本节课的学习要点，为后续的学习奠定坚实的基础。总之，这套演示文稿内容丰富、结构合理，能够有效地帮助学生掌握稍复杂的找次品问题的最优策略。通过学习目标的明确、课前导入的引导、学习任务的实践、达标练习的巩固以及知识总结的梳理，学生能够在各个环节中逐步提升自己的数学素养和解题能力。这种系统化的教学设计不仅能够提高学生的学习效率，还能培养他们的自主学习能力和创新思维能力，是一份非常实用且高效的教学资源。
-
含教案
数学北师大八年级上册第四章 一次函数 4.1函数（教学课件）ppt课件含教案
页数：21 | 大小：5M这份共二十一张幻灯片的PPT课件，专为北师大版八年级上册第四章《4.1 函数》量身定制，以“从生活现象中捕捉变化规律”为切入口，引导学生完成从“感性认识变量”到“抽象定义函数”的第一次跨越。课堂流程简洁而递进：情境导入—探究新知—典例巩固—课堂小结。 开篇“情境导入”用日常短视频串烧：自动扶梯的梯级高度与时间、加油机金额与油量、气温与海拔，三组画面同步滚动，学生边看边记录“谁跟着谁变”，教师追问“一个量确定后，另一个量是否唯一确定？”生活事例瞬间聚焦到“对应”这一核心。 “探究新知”分三步走：先给出函数描述性定义，强调“唯一对应”关键词；再借助箭头图、解析式、表格三种方式呈现同一关系，让学生直观感受函数的多元表征；最后通过“分式型、根式型、零次幂型”三类表达式，归纳求自变量取值范围的“三把钥匙”——分母不为零、偶根非负、零次底非零，每把钥匙配一道即时口答，错误答案瞬间红显，强化记忆。 “典例巩固”采用“一题多变”：同一背景“汽车匀速行驶”分别用表格、解析式、图像给出，学生抢答自变量范围并计算函数值，平板自动生成正确率柱形图，教师针对最低得分点二次讲解；随后推送两道中考真题切片，要求学生判断是否为函数关系并说明理由，实现“所学即所考”的无缝对接。 结课用“思维导图快闪”：定义、表示、求范围、求函数值四节点依次展开，学生用电子笔补充易错提示，生成班级共性记忆图；作业分两层：A层教材习题夯实基础，B层拍摄生活短视频，指出其中的自变量与函数关系并配文说明，把课堂发现带回日常。整套课件以少量幻灯片承载大容量思维，通过“视觉冲击—多元表征—即时反馈”的闭环设计，不仅让学生真正理解“函数就是对应”，更在“找范围、求值、判断关系”的实战中，为后续学习一次函数、二次函数奠定坚实的概念与技能双重根基。
-
含教案
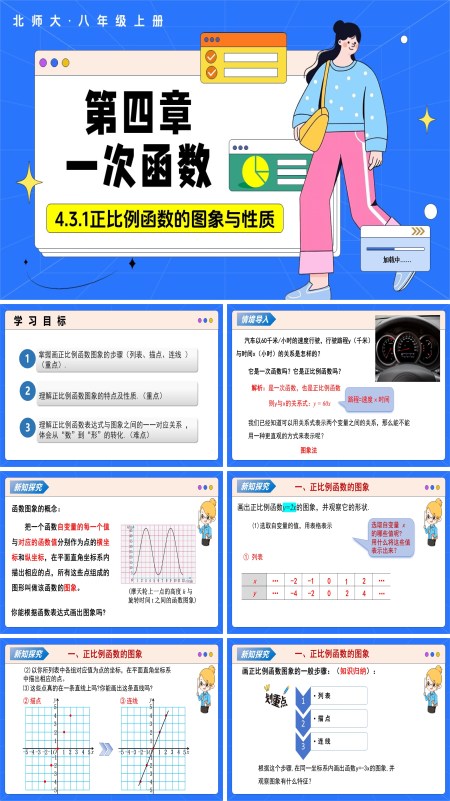
数学北师大八年级上第四章 4.3一次函数的图象（第1课时正比例函数的图象与性质）（教学课件）ppt课件含教案
页数：22 | 大小：4M这套由二十二张幻灯片构成的教学课件，专为北师大版八年级上册第四章《一次函数的图像》第一课时“正比例函数的图像与性质”量身定制，旨在让学生经历“表达式→表格→描点→连线→观察→归纳”的完整过程，真正理解“k值决定直线姿势，原点必过”的图像本质。课堂依旧四段推进：情境导入—新知探究—典例巩固—课堂小结。开篇“情境导入”给出汽车仪表盘特写：指针定格在80 km/h，屏幕动态显示行驶时间t与路程s同步增加。教师提问：“除了列表、写式，还能怎样一眼看出s=80t的变化趋势？”学生脱口而出“画图像”，生活经验瞬间对接“图像法”必要性，引出本节核心任务。“新知探究”分三步走：先回顾函数图像定义——“所有有序点（x，y）的集合”；随后聚焦正比例y=kx，学生分组填表、描点、连线，发现无论k为正为负，图像都是一条经过原点的直线；接着用GeoGebra动态拖动k值，观察直线旋转，归纳出“k0，过一、三象限，上升；k0，过二、四象限，下降；|k|越大，直线越陡”的性质口诀，实现“数形同步”。“典例巩固”采用“一题三问”：给出y=2x，先列表描点验证直线，再求x=1.5时的函数值，最后判断点（-2，-4）是否在图像上，平板实时统计正确率，教师针对红区错误现场“开刀”；随后推送中考真题切片，要求根据图像写解析式并比较k值大小，实现“所见即所考”。结课用“思维导图快闪”：列表→描点→连线→观察→归纳五节点依次展开，学生口头接龙补充易错点；作业分两层：A层完成教材配套描点画图，B层拍摄家中水龙头流水视频，记录时间与接水量，验证是否为正比例并画图像，把课堂发现带回家。整套课件通过“动态生成—即时观察—对比归纳”的闭环，不仅让学生真正理解“解析式与图像一一对应”，更在“画一画、看一看、比一比”的亲历中，深刻体会数形结合思想，为后续学习一次函数平移、斜截式及实际应用奠定坚实的图像与性质双重基础。
-
二次元倒计时创意开场动画PPT模板
页数：1 | 大小：8M这套二次元倒计时创意开场动画PPT模板设计十分俏皮，10秒倒计时中，每一个数字都采用了多种色彩的重叠组合，二次元的世界，带给您不一样的视觉效果。
-
人教版九年级上册数学《二次函数》的PPT模板
页数：20 | 大小：4MPPT模板从五个部分来展开介绍关于《二次函数》的教学内容。PPT模板的第一部分借助思维导图的形式回顾了有关函数的基础知识，并指明了本节课的两点学习目标。第二部分通过创设具体的问题情景来引导学生探究两个变量之间的关系，从而总结出其共同点。第三部分阐述了二次函数的定义，并强调了相关注意事项以及二次函数的一般形式和特殊形式。第四部分对相关例题进行分析和讲解。第五部分总结归纳了本节课的重点内容。
