人教版高中数学选择性必修二等比数列的前n项和公式 (1) 教学设计(内容完整)
Word格式/内容可修改





问题3:如何求解该问题.回顾:等差数列的前 n 项和公式的推导过程.等差数列 a_1,a_2, a_3, 〖…a〗_n的前 n项和是〖S_n=a〗_1+a_2+a_3+〖…+a〗_(n-2) 〖+a〗_(n-1) 〖+a〗_n根据等差数列的定义a_(n+1) 〖-a〗_n= d〖S_n=a〗_1+a_2+a_3+〖…+a〗_(n-2) 〖+a〗_(n-1) 〖+a〗_n ①〖S_n=a〗_n+a_(n-1)+a_(n-2)+〖…+a〗_3 〖+a〗_2 〖+a〗_1 ②①+ ②得,〖〖2S〗_n=n(a_1+a〗_n).所以S_n=(〖n(a_1+a〗_n ")." )/2问题4:对于等比数列,是否也能用倒序相加的方法进行求和呢?在等比数列中a_1 〖+a〗_n≠a_2 〖+a〗_(n-1)≠a_3 〖+a〗_(n-2),所以〖〖2S〗_n≠n(a_1+a〗_n).对于等比数列求和,不能照搬倒序相加的方法,而是要挖掘此方法的本质,即求和的根本目的.问题5:求和的根本目的是什么?思路:为了看清式子的特点,我们不妨把各项都用首项和公比来表示.〖S_n=a〗_1+a_1 q+a_2 q^2+〖…+a〗_1 q^(n-3) 〖+a〗_1 〖q^(n-2)+a〗_1 q^(n-1) ①问题6:观察① 式,相邻两项有什么特征?怎样把某一项变成它的后一项?〖a_n=a〗_(n-1) q(n≥2,q≠0)问题7:如何构造另一个式子,与原式相减后可以消除中间项?〖S_n=a〗_1+a_1 q+a_2 q^2+〖…+a〗_1 q^(n-3) 〖+a〗_1 〖q^(n-2)+a〗_1 q^(n-1) ①〖qS_n=a〗_1 q+a_1 q^2+a_2 q^3+〖…+a〗_1 q^(n-2) 〖+a〗_1 〖q^(n-1)+a〗_1 q^n ②设等比数列 {a_n } 的首项为a_1 ,公比为q ,则{a_n } 的前n项和是S_n〖S_n=a〗_1+a_2+a_3+〖…+a〗_(n-2) 〖+a〗_(n-1) 〖+a〗_n根据等比数列的通项公式,〖S_n=a〗_1+a_1 q+a_2 q^2+〖…+a〗_1 q^(n-3) 〖+a〗_1 〖q^(n-2)+a〗_1 q^(n-1) ①〖qS_n=a〗_1 q+a_1 q^2+a_2 q^3+〖…+a〗_1 q^(n-2) 〖+a〗_1 〖q^(n-1)+a〗_1 q^n ②① - ②得, S_n -qS_n=a_1 -a_1 q^n即S_n(1 -q)=a_1( 1-q^n)问题8:要求出S_n,是否可以把上式两边同时除以(1 -q) ?
转载请注明出处!本文地址:
https://www.mikeppt.com/wd/20231027095618294.html- 软件:Office 2016及以上版本
- 格式:docx
- 文件大小:632.17KB
- 页数:9
- 编号:20231027095618294
- 售价:5 金币 / 会员免费
- 上传时间:2023-10-27
- 上传者:橙子喵
- 肖像权:人物画像及字体仅供参考
-
人教版高中数学选择性必修二等比数列的前n项和公式 (1) 教学设计(内容完整)
教育教学模板 | 页数:9 -
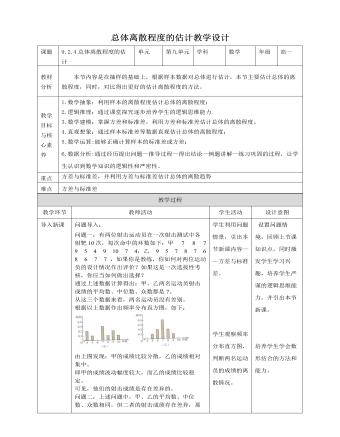
人教A版高中数学必修二总体离散程度的估计教学设计(内容完整)
教育教学模板 | 页数:8 -
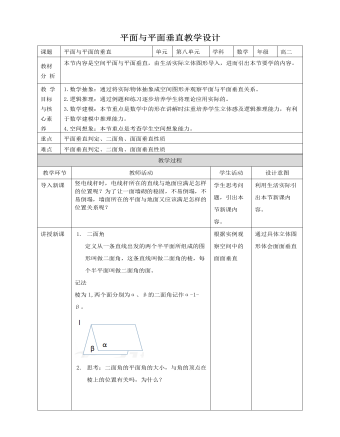
人教A版高中数学必修二平面与平面垂直教学设计(内容完整)
教育教学模板 | 页数:11 -
人教版高中数学选修3分类变量与列联表教学设计(内容完整)
教育教学模板 | 页数:19 -
人教版高中数学选择性必修二等比数列的前n项和公式 (2) 教学设计(内容丰富)
教育教学模板 | 页数:8 -
新人教版高中英语选修2Unit 3 Using langauge-Listening教学设计(内容完整)
教育教学模板 | 页数:5 -
人教版高中数学选择性必修二等比数列的概念 (1) 教学设计(内容全面)
教育教学模板 | 页数:9